Signal Modelling

The steady-state longitudinal magnetization of an inversion recovery experiment can be derived from the Bloch equations for the pulse sequence {θ180 – TI – θ90 – (TR-TI)}, and is given by:

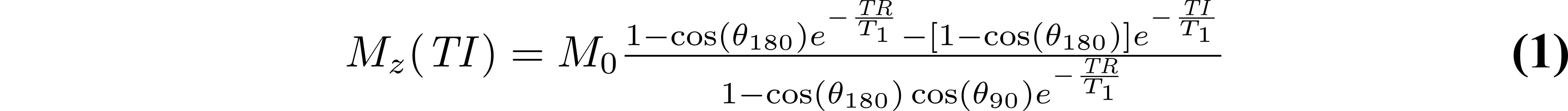
where Mz is the longitudinal magnetization prior to the θ90 pulse. If the in-phase real signal is desired, it can be calculated by multiplying Eq. 1 by ksin(θ90)e-TE/T2, where k is a constant. This general equation can be simplified by grouping together the constants for each measurements regardless of their values (i.e. at each TI, same TE and θ90 are used) and assuming an ideal inversion pulse:

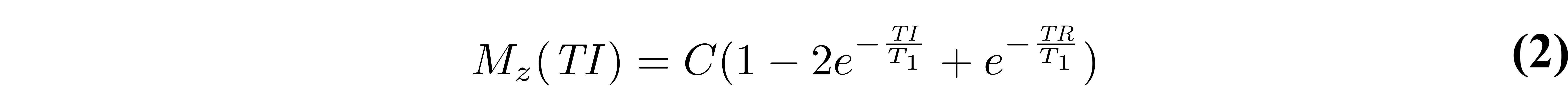
where the first three terms and the denominator of Eq. 1 have been grouped together into the constant C. If the experiment is designed such that TR is long enough to allow for full relaxation of the magnetization (TR > 5T1), we can do an additional approximation by dropping the last term in Eq. 2:

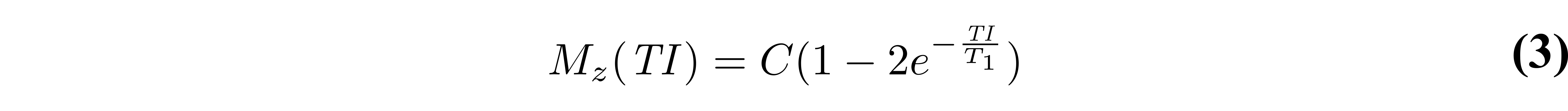
The simplicity of the signal model described by Eq. 3, both in its equation and experimental implementation, has made it the most widely used equation to describe the signal evolution in an inversion recovery T1 mapping experiment. The magnetization curves are plotted in Figure 2 for approximate T1 values of three different tissues in the brain. Note that in many practical implementations, magnitude-only images are acquired, so the signal measured would be proportional to the absolute value of Eq. 3.

Figure 2. Inversion recovery curves (Eq. 2) for three different T1 values, approximating the main types of tissue in the brain. 

%use octave

% Verbosity level 0 overrides the disp function and supresses warnings.
% Once executed, they cannot be restored in this session
% (kernel needs to be restarted or a new notebook opened.)
VERBOSITY_LEVEL = 0;

if VERBOSITY_LEVEL==0
    % This hack was used to supress outputs from external tools
    % in the Jupyter Book.
    function disp(x)
    end
    warning('off','all')
end

try
    cd qMRLab
catch
    try
        cd ../../qMRLab
    catch
        cd ../qMRLab
    end
end

startup
clear all

%% Setup parameters
% All times are in seconds
% All flip angles are in degrees

params.TR = 5.0;
params.TI = linspace(0.001, params.TR, 1000);
            
params.TE = 0.004;
params.T2 = 0.040;
            
params.EXC_FA = 90;  % Excitation flip angle
params.INV_FA = 180; % Inversion flip angle

params.signalConstant = 1;

%% Calculate signals
%
% The option 'GRE-IR' selects the analytical equations for the
% gradient echo readout inversion recovery experiment The option
% '4' is a flag that selects the long TR approximation of the 
% analytical solution (TR>>T1), Eq. 3 of the blog post.
%
% To see all the options available, run:
% `help inversion_recovery.analytical_solution`

% White matter
params.T1 = 0.900; % in seconds

signal_WM = inversion_recovery.analytical_solution(params, 'GRE-IR', 4);

% Grey matter
params.T1 = 1.500;  % in seconds
signal_GM = inversion_recovery.analytical_solution(params, 'GRE-IR', 4);

% CSF
params.T1 = 4.000;  % in seconds
signal_CSF = inversion_recovery.analytical_solution(params, 'GRE-IR', 4);

(View simulation code) 

%use sos
%get params --from Octave
%get signal_WM --from Octave
%get signal_GM --from Octave
%get signal_CSF --from Octave

import matplotlib.pyplot as plt
import plotly.plotly as py
import plotly.graph_objs as go
import numpy as np
from plotly import __version__
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
config={'showLink': False, 'displayModeBar': False}

init_notebook_mode(connected=True)

from IPython.core.display import display, HTML

wm = go.Scatter(
    x = params["TI"],
    y = signal_WM,
    name = 'T<sub>1</sub> = 0.9 s (White Matter)',
    text = 'T<sub>1</sub> = 0.9 s (White Matter)',
    hoverinfo = 'x+y+text'
)

gm = go.Scatter(
    x = params["TI"],
    y = signal_GM,
    name = 'T<sub>1</sub> = 1.5 s (Grey Matter)',
    text = 'T<sub>1</sub> = 1.5 s (Grey Matter)',
    hoverinfo = 'x+y+text'
)

csf = go.Scatter(
    x = params["TI"],
    y = signal_CSF,
    name = 'T<sub>1</sub> = 4.0 s (Cerebrospinal Fluid)',
    text = 'T<sub>1</sub> = 4.0 s (Cerebrospinal Fluid)',
    hoverinfo = 'x+y+text'
)

data = [wm, gm, csf]

layout = go.Layout(
    width=600,
    height=350,
    margin=go.layout.Margin(
        l=100,
        r=50,
        b=60,
        t=0,
    ),
    annotations=[
        dict(
            x=0.5004254919715793,
            y=-0.175,
            showarrow=False,
            text='Inversion Time – TI (ms)',
            font=dict(
                family='Times New Roman',
                size=22
            ),
            xref='paper',
            yref='paper'
        ),
        dict(
            x=-0.15,
            y=0.50,
            showarrow=False,
            text='Long. Magnetization (M<sub>z</sub>)',
            font=dict(
                family='Times New Roman',
                size=22
            ),
            textangle=-90,
            xref='paper',
            yref='paper'
        ),
    ],
    xaxis=dict(
        showgrid=False,
        linecolor='black',
        linewidth=2
    ),
    yaxis=dict(
        showgrid=False,
        linecolor='black',
        linewidth=2
    ),
    legend=dict(
        x=0.55,
        y=0.15,
        traceorder='normal',
        font=dict(
            family='Times New Roman',
            size=12,
            color='#000'
        ),
        bordercolor='#000000',
        borderwidth=2
    )
)

fig = dict(data=data, layout=layout)

plot(fig, filename = 'ir_fig_2.html', config = config)

display(HTML('ir_fig_2.html'))

(View plot code)

Practically, Eq. 1 is the better choice for simulating the signal of an inversion recovery experiment, as the TRs are often chosen to be greater than 5T1 of the tissue-of-interest, which rarely coincides with the longest T1 present (e.g. TR may be sufficiently long for white matter, but not for CSF which could also be present in the volume). Equation 3 also assumes ideal inversion pulses, which is rarely the case due to slice profile effects. Figure 3 displays the inversion recovery signal magnitude (complete relaxation normalized to 1) of an experiment with TR = 5 s and T1 values ranging between 250 ms to 5 s, calculated using both equations.

Figure 3. Signal recovery curves simulated using Eq. 3 (solid) and Eq. 1 (dotted) with a TR = 5 s for T1 values ranging between 0.25 to 5 s. 

%use octave

% Verbosity level 0 overrides the disp function and supresses warnings.
% Once executed, they cannot be restored in this session
% (kernel needs to be restarted or a new notebook opened.)
VERBOSITY_LEVEL = 0;

if VERBOSITY_LEVEL==0
    % This hack was used to supress outputs from external tools
    % in the Jupyter Book.
    function disp(x)
    end
    warning('off','all')
end

try
    cd qMRLab
catch
    try
        cd ../../qMRLab
    catch
        cd ../qMRLab
    end
end

startup
clear all

%% Setup parameters
% All times are in seconds
% All flip angles are in degrees

params.TR = 5.0;
params.TI = linspace(0.001, params.TR, 1000);
            
params.TE = 0.004;
params.T2 = 0.040;
            
params.EXC_FA = 90;  % Excitation flip angle
params.INV_FA = 180; % Inversion flip angle

params.signalConstant = 1;

T1_range = 0.25:0.25:5; % in seconds

%% Calculate signals
%
% The option 'GRE-IR' selects the analytical equations for the
% gradient echo readout inversion recovery experiment. The option
% '1' is a flag that selects full analytical solution equation 
% (no approximation), Eq. 1 of the blog post. The option '4' is a
% flag that selects the long TR approximation of the analytical 
% solution (TR>>T1), Eq. 3 of the blog post.
%
% To see all the options available, run:
% `help inversion_recovery.analytical_solution`

for ii = 1:length(T1_range)
    params.T1 = T1_range(ii);
    
    signal_T1_Eq1{ii} = inversion_recovery.analytical_solution(params, 'GRE-IR', 1);

    signal_T1_Eq3{ii} = inversion_recovery.analytical_solution(params, 'GRE-IR', 4);
end

(View simulation code) 

%use sos
%get T1_range --from Octave
%get signal_T1_Eq1 --from Octave
%get signal_T1_Eq3 --from Octave

import matplotlib.pyplot as plt
import plotly.plotly as py
import plotly.graph_objs as go
import numpy as np
from plotly import __version__
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
config={'showLink': False, 'displayModeBar': False}

init_notebook_mode(connected=True)

from IPython.core.display import display, HTML

data1 = [dict(
        visible = False,
        x = params["TI"],
        y = abs(signal_T1_Eq3[ii]),
        name = '[Eq. 3] – Long TR approximation',
        text = '[Eq. 3] – Long TR approximation',
        hoverinfo = 'x+y+text') for ii in range(len(T1_range))]

data1[3]['visible'] = True

data2 = [dict(
        visible = False,
        x = params["TI"],
        y = abs(signal_T1_Eq1[ii]),
        line = dict(
            color = ('rgb(22, 96, 167)'),
            dash = 'dash'),
        name = '[Eq. 1] – General Equation',
        text = '[Eq. 1] – General Equation',
        hoverinfo = 'x+y+text') for ii in range(len(T1_range))]

data2[3]['visible'] = True

data = data1 + data2

steps = []
for i in range(len(T1_range)):
    step = dict(
        method = 'restyle',  
        args = ['visible', [False] * len(data1)],
        label = str(T1_range[i])
    )
    step['args'][1][i] = True # Toggle i'th trace to "visible"
    steps.append(step)

sliders = [dict(
    x = 0,
    y = -0.0,
    active = 3,
    currentvalue = {"prefix": "T<sub>1</sub> value (s): <b>"},
    pad = {"t": 50, "b": 10},
    steps = steps
)]

layout = go.Layout(
    width=580,
    height=400,
    margin=go.layout.Margin(
        l=80,
        r=40,
        b=60,
        t=10,
    ),
    annotations=[
        dict(
            x=0.5004254919715793,
            y=-0.2,
            showarrow=False,
            text='Inversion Time – TI (ms)',
            font=dict(
                family='Times New Roman',
                size=22
            ),
            xref='paper',
            yref='paper'
        ),
        dict(
            x=-0.14,
            y=0.5,
            showarrow=False,
            text='Signal (magnitude)',
            font=dict(
                family='Times New Roman',
                size=22
            ),
            textangle=-90,
            xref='paper',
            yref='paper'
        ),
    ],
    xaxis=dict(
        autorange=False,
        range=[0, 5],
        showgrid=False,
        linecolor='black',
        linewidth=2
    ),
    yaxis=dict(
        autorange=False,
        range=[0, 1],
        showgrid=False,
        linecolor='black',
        linewidth=2
    ),
    legend=dict(
        x=0.5,
        y=0.5,
        traceorder='normal',
        font=dict(
            family='Times New Roman',
            size=12,
            color='#000'
        ),
        bordercolor='#000000',
        borderwidth=2
    ), 
    sliders=sliders
)

fig = dict(data=data, layout=layout)

plot(fig, filename = 'ir_fig_3.html', config = config)
display(HTML('ir_fig_3.html'))

(View plot code)