Signal Modelling
The steady-state longitudinal magnetization of an ideal variable flip angle experiment can be analytically solved from the Bloch equations for the spoiled gradient echo pulse sequence {θn–TR}:
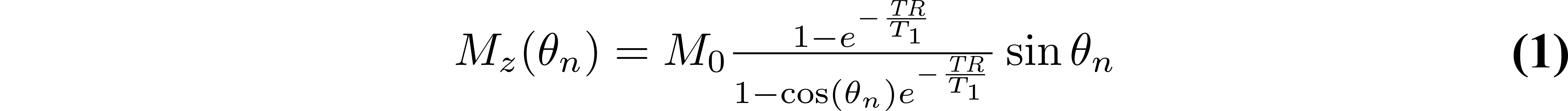
where Mz is the longitudinal magnetization, M0 is the magnetization at thermal equilibrium, TR is the pulse sequence repetition time (Figure 1), and θn is the excitation flip angle. The Mz curves of different T1 values for a range of θn and TR values are shown in Figure 2.
Figure 2. Variable flip angle technique signal curves (Eq. 1) for three different T1 values, approximating the main types of tissue in the brain at 3T.
(View simulation code)
(View plotting code)
From Figure 2, it is clearly seen that the flip angle at which the steady-state signal is maximized is dependent on the T1 and TR values. This flip angle is a well known quantity, called the Ernst angle (Ernst & Anderson 1966), which can be solved analytically from Equation 1 using properties of calculus:
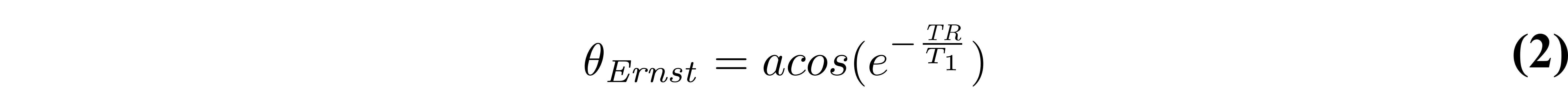
The closed-form solution (Equation 1) makes several assumptions which in practice may not always hold true if care is not taken. Mainly, it is assumed that the longitudinal magnetization has reached a steady state after a large number of TRs, and that the transverse magnetization is perfectly spoiled at the end of each TR. Bloch simulations – a numerical approach at solving the Bloch equations for a set of spins at each time point – provide a more realistic estimate of the signal if the number of repetition times is small (i.e. a steady-state is not achieved). As can be seen from Figure 3, the number of repetitions required to reach a steady state not only depends on T1, but also on the flip angle; flip angles near the Ernst angle need more TRs to reach a steady state. Preparation pulses or an outward-in k-space acquisition pattern are typically sufficient to reach a steady state by the time that the center of k-space is acquired, which is where most of the image contrast resides.
Figure 3. Signal curves simulated using Bloch simulations (orange) for a number of repetitions ranging from 1 to 150, plotted against the ideal case (Equation 1 – blue). Simulation details: TR = 25 ms, T1 = 900 ms, 100 spins. Ideal spoiling was used for this set of Bloch simulations (transverse magnetization was set to 0 at the end of each TR).
(View simulation code)
(View plot code)
Sufficient spoiling is likely the most challenging parameter to control for in a VFA experiment. A combination of both gradient spoiling and RF phase spoiling (Zur et al. 1991; Bernstein et al. 2004) are typically recommended (Figure 4). It has also been shown that the use of very strong gradients, introduces diffusion effects (not considered in Figure 4), further improving the spoiling efficacy in the VFA pulse sequence (Yarnykh 2010).
Figure 4. Signal curves estimated using Bloch simulations for three categories of signal spoiling: (1) ideal spoiling (blue), gradient & RF Spoiling (orange), and no spoiling (green). Simulations details: TR = 25 ms, T1 = 900 ms, Te = 100 ms, TE = 5 ms, 100 spins. For the ideal spoiling case, the transverse magnetization is set to zero at the end of each TR. For the gradient & RF spoiling case, each spin is rotated by different increments of phase (2𝜋 / # of spins) to simulate complete decoherence from gradient spoiling, and the RF phase of the excitation pulse is ɸn = ɸn-1 + nɸ0 = ½ ɸ0(n2 + n + 2) (Bernstein et al. 2004) with ɸ0 = 117° (Zur et al. 1991) after each TR.
(View simulation code)
(View plot code)