Data Fitting
At first glance, one could be tempted to fit VFA data using a non-linear least squares fitting algorithm such as Levenberg-Marquardt with Eq. 1, which typically only has two free fitting variables (T1 and M0). Although this is a valid way of estimating T1 from VFA data, it is rarely done in practice because a simple refactoring of Equation 1 allows T1 values to be estimated with a linear least square fitting algorithm, which substantially reduces the processing time. Without any approximations, Equation 1 can be rearranged into the form y = mx+b (Gupta 1977):
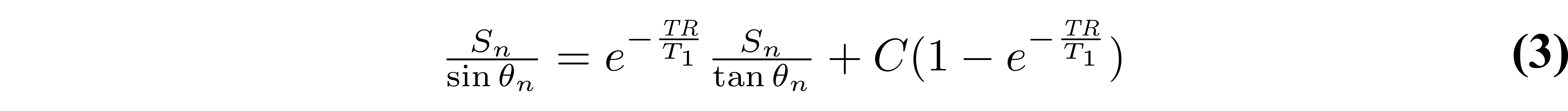
As the third term does not change between measurements (it is constant for each θn), it can be grouped into the constant for a simpler representation:
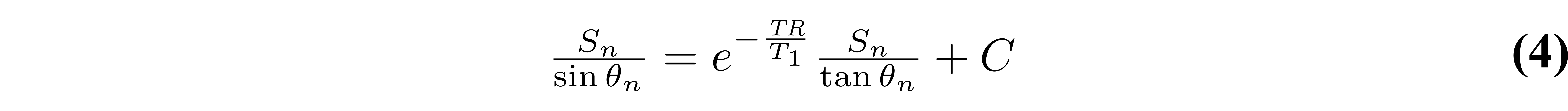
With this rearranged form of Equation 1, T1 can be simply estimated from the slope of a linear regression calculated from Sn/sin(θn) and Sn/tan(θn) values:
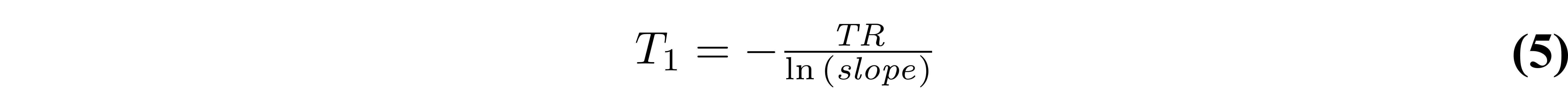
If data were acquired using only two flip angles – a very common VFA acquisition protocol – then the slope can be calculated using the elementary slope equation. Figure 5 displays both Equation 1 and 4 plotted for a noisy dataset.
Figure 5. Mean and standard deviation of the VFA signal plotted using the nonlinear form (Equation 1 – blue) and linear form (Equation 4 – red). Monte Carlo simulation details: SNR = 25, N = 1000. VFA simulation details: TR = 25 ms, T1 = 900 ms.
(View simulation code)
(View plot code)
There are two important imaging protocol design considerations that should be taken into account when planning to use VFA: (1) how many and which flip angles to use to acquire VFA data, and (2) correcting inaccurate flip angles due to transmit RF field inhomogeneity. Most VFA experiments use the minimum number of required flip angles (two) to minimize acquisition time. For this case, it has been shown that the flip angle choice resulting in the best precision for VFA T1 estimates for a sample with a single T1 value (i.e. single tissue) are the two flip angles that result in 71% of the maximum possible steady-state signal (i.e. at the Ernst angle) (Deoni et al. 2003; Schabel & Morrell 2009).
Time allowing, additional flip angles are often acquired at higher values and in between the two above, because greater signal differences between tissue T1 values are present there (e.g. Figure 2). Also, for more than two flip angles, Equations 1 and 4 do not have the same noise weighting for each fitting point, which may bias linear least-square T1 estimates at lower SNRs. Thus, it has been recommended that low SNR data should be fitted with either Equation 1 using non-linear least-squares (slower fitting) or with a weighted linear least-squares form of Equation 4 (Chang et al. 2008).
Accurate knowledge of the flip angle values is very important to produce accurate T1 maps. Because of how the RF field interacts with matter (Sled & Pike 1998), the excitation RF field (B1+, or B1 for short) of a loaded RF coil results in spatial variations in intensity/amplitude, unless RF shimming is available to counteract this effect (not common at clinical field strengths). For quantitative measurements like VFA which are sensitive to this parameter, the flip angle can be corrected (voxelwise) relative to the nominal value by multiplying it with a scaling factor (B1) from a B1 map that is acquired during the same session:
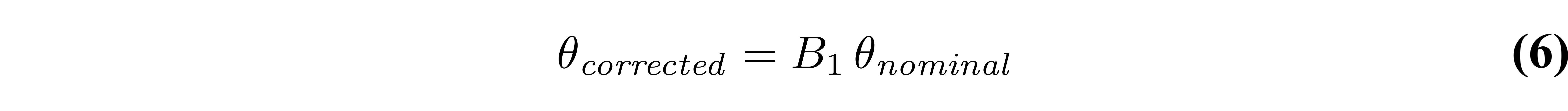
B1 in this context is normalized, meaning that it is unitless and has a value of 1 in voxels where the RF field has the expected amplitude (i.e. where the nominal flip angle is the actual flip angle). Figure 6 displays fitted VFA T1 values from a Monte Carlo dataset simulated using biased flip angle values, and fitted without/with B1 correction.
Figure 6. Mean and standard deviations of fitted VFA T1 values for a set of Monte Carlo simulations (SNR = 100, N = 1000), simulated using a wide range of biased flip angles and fitted without (blue) or with (red) B1 correction. Simulation parameters: TR = 25 ms, T1 = 900 ms, θnominal = 6° and 32° (optimized values for this TR/T1 combination). Notice how even after B1 correction, fitted T1 values at B1 values far from the nominal case (B1 = 1) exhibit larger variance, as the actual flip angles of the simulated signal deviate from the optimal values for this TR/T1 (Deoni et al. 2003).
(View simulation code)
(View plot code)
Figure 7 displays an example VFA dataset and a B1 map in a healthy brain, along with the T1 map estimated using a linear fit (Equations 4 and 5).
Figure 7. Example variable flip angle dataset and B1 map of a healthy adult brain (left). The relevant VFA protocol parameters used were: TR = 15 ms, θnominal = 3° and 20°. The T1 map (right) was fitted using a linear regression (Equations 4 and 5).
(View fitting code)
(View plot code)