Data Fitting
Several factors impact the choice of the inversion recovery fitting algorithm. If only magnitude images are available, then a polarity-inversion is often implemented to restore the non-exponential magnitude curves (Figure 3) into the exponential form (Figure 2). This process is sensitive to noise due to the Rician noise creating a non-zero level at the signal null. If phase data is also available, then a phase term must be added to the fitting equation (Barral et al. 2010). Equation 3 must only be used to fit data for the long TR regime (TR > 5T1), which in practice is rarely satisfied for all tissues in subjects.
Early implementations of inversion recovery fitting algorithms were designed around the computational power available at the time. These included the “null method” (Pykett et al. 1983), assuming that each T1 value has unique zero-crossings (see Figure 2), and linear fitting of a rearranged version of Eq. 3 on a semi-log plot (Fukushima & Roeder 1981). Nowadays, a non-linear least-squares fitting algorithm (e.g. Levenberg-Marquardt) is more appropriate, and can be applied to either approximate or general forms of the signal model (Eq. 3 or Eq. 1). More recent work (Barral et al. 2010) demonstrated that T1 maps can also be fitted much faster (up to 75 times compared to Levenberg-Marquardt) to fit Eq. 1 – without a precision penalty – by using a reduced-dimension non-linear least squares (RD-NLS) algorithm. It was demonstrated that the following simplified 5-parameter equation can be sufficient for accurate T1 mapping:
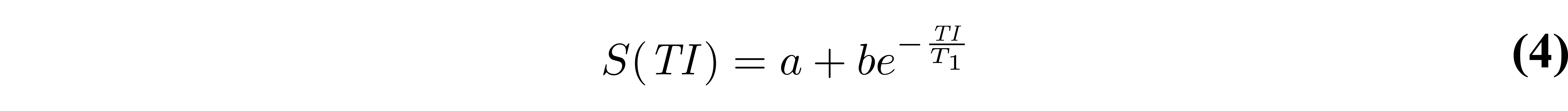
where a and b are complex values. If magnitude-only data is available, a 3-parameter model can be sufficient by taking the absolute value of Eq. 4. While the RD-NLS algorithms are too complex to be presented here (the reader is referred to the paper, (Barral et al. 2010)), the code for these algorithms was released open-source along with the original publication, and is also available as a qMRLab T1 mapping model. One important thing to note about Eq. 4 is that it is general – no assumption is made about TR – and is thus as robust as Eq. 1 as long as all pulse sequence parameters other than TI are kept constant between each measurement. Figure 4 compares simulated data (Eq. 1) using a range of TRs (1.5T1 to 5T1) fitted using either RD-NLS & Eq. 4 or a Levenberg-Marquardt fit of Eq. 2.
Figure 4. Fitting comparison of simulated data (blue markers) with T1 = 1 s and TR = 1.5 to 5 s, using fitted using RD-NLS & Eq. 4 (green) and Levenberg-Marquardt & Eq. 2 (orange, long TR approximation).
(View simulation code)
(View plot code)
Figure 5 displays an example brain dataset from an inversion recovery experiment, along with the T1 map fitted using the RD-NLS technique.
Figure 5. Example inversion recovery dataset of a healthy adult brain (left). Inversion times used to acquire this magnitude image dataset were 30 ms, 530 ms, 1030 ms, and 1530 ms, and the TR used was 1550 ms. The T1 map (right) was fitted using a RD-NLS algorithm.
(View fitting code)
(View plot code)