.ipynb .pdf

repository open issue

Binder Live Code

Contents

T1, MTR and MTsat in-vivo

3 healthy participants were scanned with the following MTsat protocol:

Click here to reveal the MTsat protocol.

Parameter (PDw/MTw/T1w)	G1NATIVE	S1NATIVE	S2NATIVE	VENUS
Sequence Name	SPGR	FLASH	FLASH	mt_sat v1.0
Flip Angle (°)	6/6/20	6/6/20	6/6/20	6/6/20
TR (ms)	32/32/18	32/32/18	32/32/18	32/32/18
TE (ms)	4	4	4	4
FOV (cm)	25.6	25.6	25.6	25.6
Acquisition Matrix	256x256	256x256	256x256	256x256
Receiver BW (kHz)	62.5	62.5	62.5	62.5
RF Phase Increment (°)	115.4	50	50	117
MT Pulse	off/on/off	off/on/off	off/on/off	off/on/off
MT Pulse Duration (ms)	8	10	10	12
MT Pulse Shape	Fermi	Gaussian	Gaussian	Fermi
MT Pulse Offset (Hz)	1200	1200	1200	1200

The following code cell loads all the necessary Python packages, defines common functions and downloads the data to /tmp/VENUS directory. If data already exists, the download will be skipped.

The number of data points per kernel-density estimations (KDE) were limited to 10k for faster visualization. Lower and upper limits of the distributions are set according to the original publication.

Tip

• You can use the legend on the right to display a selection of KDEs. For example, double click on G1_VENUS to single out vendor-neutral distributions acquired on the GE scanner.

• At the top right corner of the plot background, you can switch the hover mode to compare data on hover to compare KDEs point by point.

import plotly.graph_objs as go
import plotly.express as px
from plotly import tools, subplots
import numpy as np
import pandas as pd
import ipywidgets as widgets
import math
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
from ipywidgets import interact, interactive, fixed, interact_manual
from IPython.core.display import display, HTML
init_notebook_mode(connected=True)
import scipy.io as sio
import random
random.seed(123)
from plotly.subplots import make_subplots

from repo2data.repo2data import Repo2Data
import os 
data_req_path = os.path.join("..", "binder", "data_requirement.json")
repo2data = Repo2Data(data_req_path)
data_path = repo2data.install()[0]
derivativesDir = os.path.join(data_path,"qMRFlow")

sessions = ['vendor750rev','vendorPRIrev','vendorSKYrev',
           'rth750rev','rthPRIrev','rthSKYrev']
sides = ["negative","negative","negative","positive","positive","positive"]
pointpos = [0,0,-0.14,0.14,0,0]
convert_tag = {'rth750':'G1<sub>VENUS</sub>','rthPRI':'S1<sub>VENUS</sub>','rthSKY':'S2<sub>VENUS</sub>',
               'vendor750':'G1<sub>NATIVE</sub>','vendorPRI':'S1<sub>NATIVE</sub>','vendorSKY':'S2<sub>NATIVE</sub>'}
colors = {'rth750':'rgba(255,8,30,1)','rthPRI':'rgba(255,117,0,1)','rthSKY':'rgba(255,220,0,1)',
         'vendor750':'rgba(0,75,255,1)','vendorPRI':'rgba(24,231,234,1)','vendorSKY':'rgba(24,234,141,1)'}
colors_line = {'rth750':'rgba(255,8,30,0.35)','rthPRI':'rgba(255,117,0,0.35)','rthSKY':'rgba(255,220,0,0.35)',
         'vendor750':'rgba(0,75,255,0.35)','vendorPRI':'rgba(24,231,234,0.35)','vendorSKY':'rgba(24,234,141,0.35)'}

def plot_ridgelines(subject,sessions,metric,region,colors,sides,sampN,leg,lowlim,uplim):
    df = pd.DataFrame()
    traces = []
    for jj in range(0,len(sessions),1):
        avg_array  = []
        std_array  =  []
        cur_region = derivativesDir + '/sub-' + subject  + '/ses-' + sessions[jj] + '/stat/sub-' + subject + '_ses-' + sessions[jj] + '_desc-' + region + '_metrics.mat'
        cur_contents = sio.loadmat(cur_region)
        cur_contents = cur_contents[metric]
        cur_contents = np.delete(cur_contents, np.where(cur_contents < lowlim))
        cur_contents = np.delete(cur_contents, np.where(cur_contents > uplim))
        cur_tag = sessions[jj][0:-3]
        cur_contents = random.sample(list(cur_contents),sampN)
        traces.append(go.Violin(
            x=cur_contents,
            name = convert_tag[cur_tag],
            marker=dict(
            opacity = 0.7,    
            outliercolor='rgba(255, 255, 255, 0.6)',
            line=dict(
                outliercolor='rgba(219, 64, 82, 0.6)',
                outlierwidth=2)),
            line_color= colors[cur_tag],
            legendgroup= convert_tag[cur_tag],
            showlegend=leg,
            side=sides[jj],
            pointpos = pointpos[jj]))
    return traces

def plot_mosaic(metric,axis_title,lowlim,uplim):
    nSamp = 10000
    traces1 = plot_ridgelines('invivo1',sessions,metric,'wm',colors,sides,nSamp,True,lowlim,uplim)
    traces2 = plot_ridgelines('invivo1',sessions,metric,'gm',colors,sides,nSamp,False,lowlim,uplim)
    traces3 = plot_ridgelines('invivo2',sessions,metric,'wm',colors,sides,nSamp,False,lowlim,uplim)
    traces4 = plot_ridgelines('invivo2',sessions,metric,'gm',colors,sides,nSamp,False,lowlim,uplim)
    traces5 = plot_ridgelines('invivo3',sessions,metric,'wm',colors,sides,nSamp,False,lowlim,uplim)
    traces6 = plot_ridgelines('invivo3',sessions,metric,'gm',colors,sides,nSamp,False,lowlim,uplim)
    fig = make_subplots(rows=3, cols=2,
                   subplot_titles=("P1 White Matter", "P1 Gray Matter", "P2 White Matter", "P2 Gray Matter", "P3 White Matter", "P3 Gray Matter"),
                   vertical_spacing = 0.08,
                   shared_xaxes=True)
    for trace in traces1:
        fig.add_trace(trace,row=1, col=1)
    for trace in traces2:
        fig.add_trace(trace,row=1, col=2)
    for trace in traces3:
        fig.add_trace(trace,row=2, col=1)
    for trace in traces4:
        fig.add_trace(trace,row=2, col=2)
    for trace in traces5:
        fig.add_trace(trace,row=3, col=1)
    for trace in traces6:
        fig.add_trace(trace,row=3, col=2)
    axis_template = dict(linecolor = 'white', 
                     showticklabels = True,
                     tickfont=dict(color="white",size=12), 
                     gridcolor = 'rgba(255,255,255,0.2)')
    fig.update_yaxes(axis_template,showgrid=False)
    fig.update_traces(orientation='h')
    fig.update_layout(paper_bgcolor = '#1c2a3d',plot_bgcolor = '#1c2a3d')
    fig.update_traces(meanline=dict(visible=True,color="white",width=3),
                      points= 'outliers', # show all points
                      jitter=0.1,
                      width=3)  # add some jitter on points for better visibility
                      #scalemode='count')
    fig.update_xaxes(axis_template)
    fig.update_layout(width=800,height=950,title=f"VENUS vs NATIVE in-vivo {metric} distributions for each participant (P)", title_font_color="white")
    fig.update_annotations(font=dict(color="white", family = "Courier"))
    for i in range(1,7): 
        fig['layout']['xaxis{}'.format(i)]['title']= axis_title
    fig.for_each_xaxis(lambda axis: axis.title.update(font=dict(color = 'white', size=12,family="Courier"),standoff=0))
    fig.update_layout(
        legend=dict(
            y = 0.5,
            font=dict(
                family="Courier",
                size=16,
                color="white")))
    return fig

import warnings
warnings.filterwarnings('ignore')

---- repo2data starting ----
/Users/agah/opt/anaconda3/envs/jbnew/lib/python3.6/site-packages/repo2data
Config from file :
../binder/data_requirement.json
Destination:
/tmp/VENUS

Info : /tmp/VENUS already downloaded

VENUS vs NATIVE T1 distributions

Note

Reproduces Figure 5d-g from the article for the Participant-3.

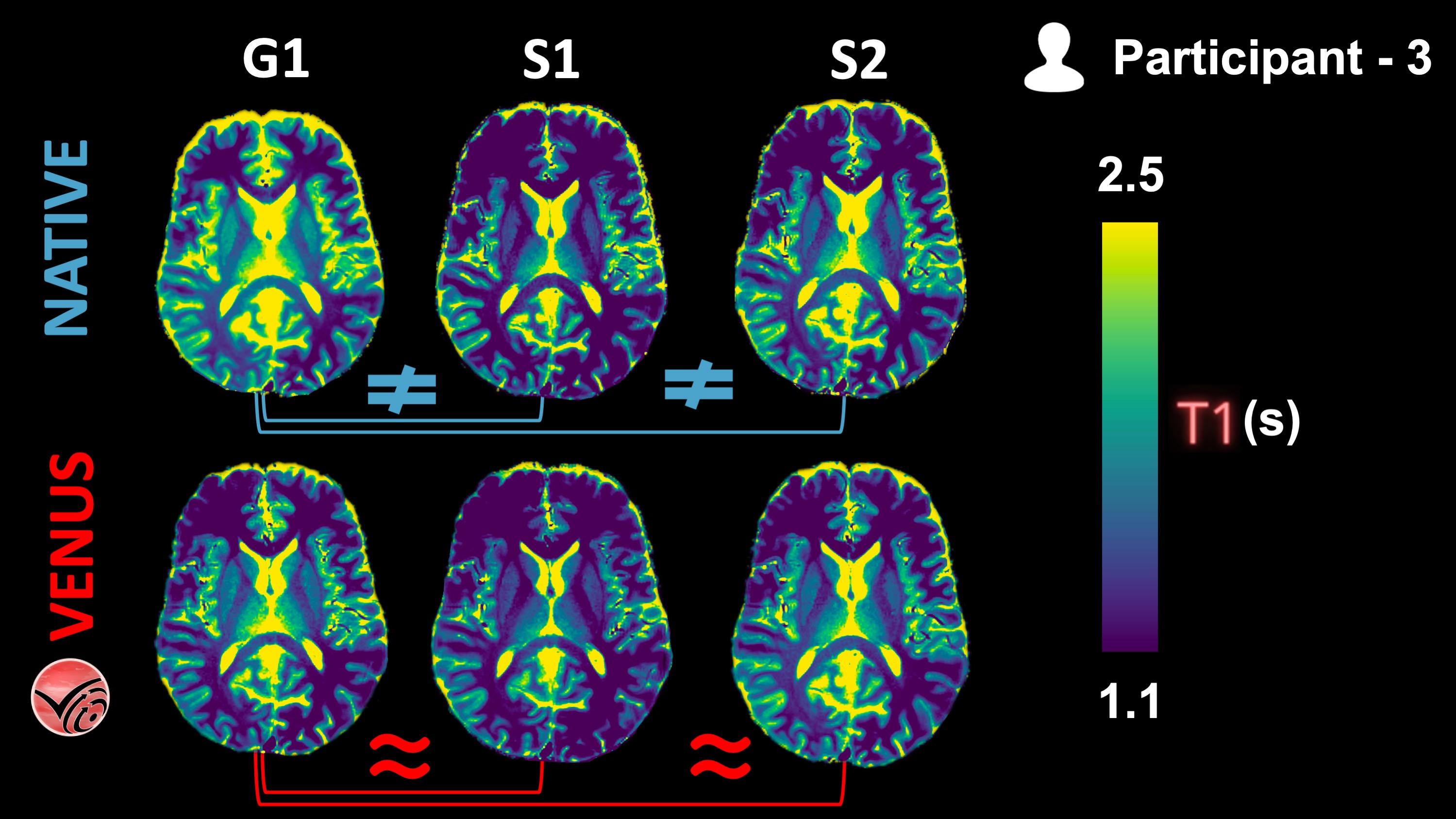
Fig. 1 vendor-native and VENUS quantitative T1 maps from P3 are shown in one axial slice.

The following KDEs agree well with the qualitative observations from the Fig. 1 above: Inter-vendor agreement (G1-vs-S1 and G1-vs-S2) of VENUS is superior to that of vendor-native T1 maps, both in the GM and WM.

fig =  plot_mosaic('T1','T1 (s)',0.5,3)
fig.show()

VENUS vs NATIVE MTR distributions

Note

Reproduces Figure 5e-h from the article for the Participant-3.

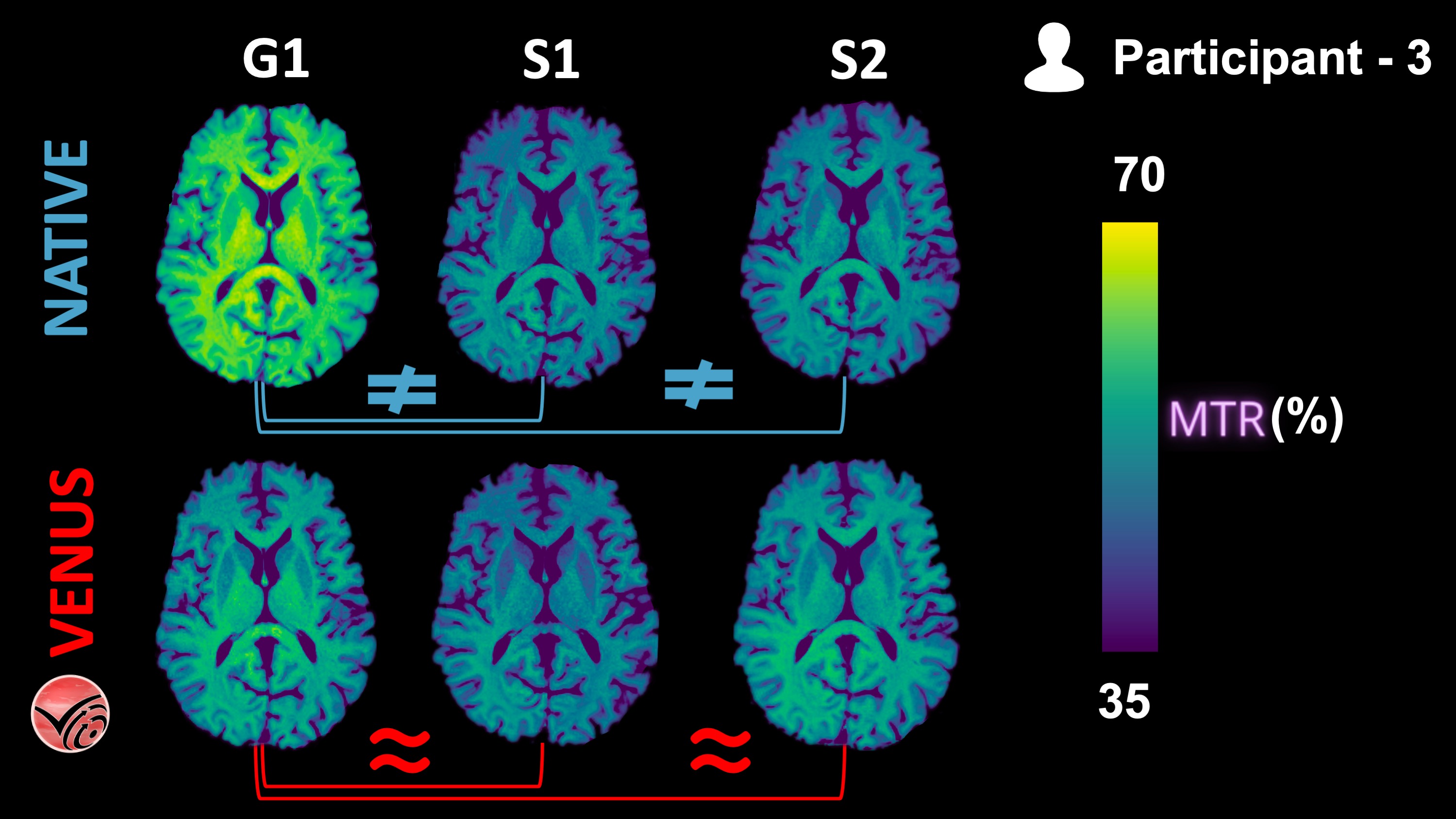
Fig. 2 nendor-native and VENUS quantitative MTR maps from P3 are shown in one axial slice.

The following KDEs agree well with the qualitative observations from the Fig. 2 above: Inter-vendor agreement (G1-vs-S1 and G1-vs-S2) of VENUS is superior to that of vendor-native MTR maps, both in the GM and WM.

fig =  plot_mosaic('MTR','MTR (%)',35,70)
fig.show()

VENUS vs NATIVE MTsat distributions

Note

Reproduces Figure 5f-i from the article for the Participant-3.

Fig. 3 vendor-native and VENUS quantitative MTsat maps from P3 are shown in one axial slice.

The following KDEs agree well with the qualitative observations from the Fig. 3 above: Inter-vendor agreement (G1-vs-S1 and G1-vs-S2) of VENUS is superior to that of vendor-native MTsat maps, both in the GM and WM.

fig =  plot_mosaic('MTsat','MTsat (a.u.)',0.5,5)
fig.show()

Deciles and shift function

Note

Reproduces Figure 6a from the article.

Before moving on to the next page that performs shift function (for P3) and hierarchical shift function analyses (across participants) in R, this subsection provides some background information about these statistical tests.

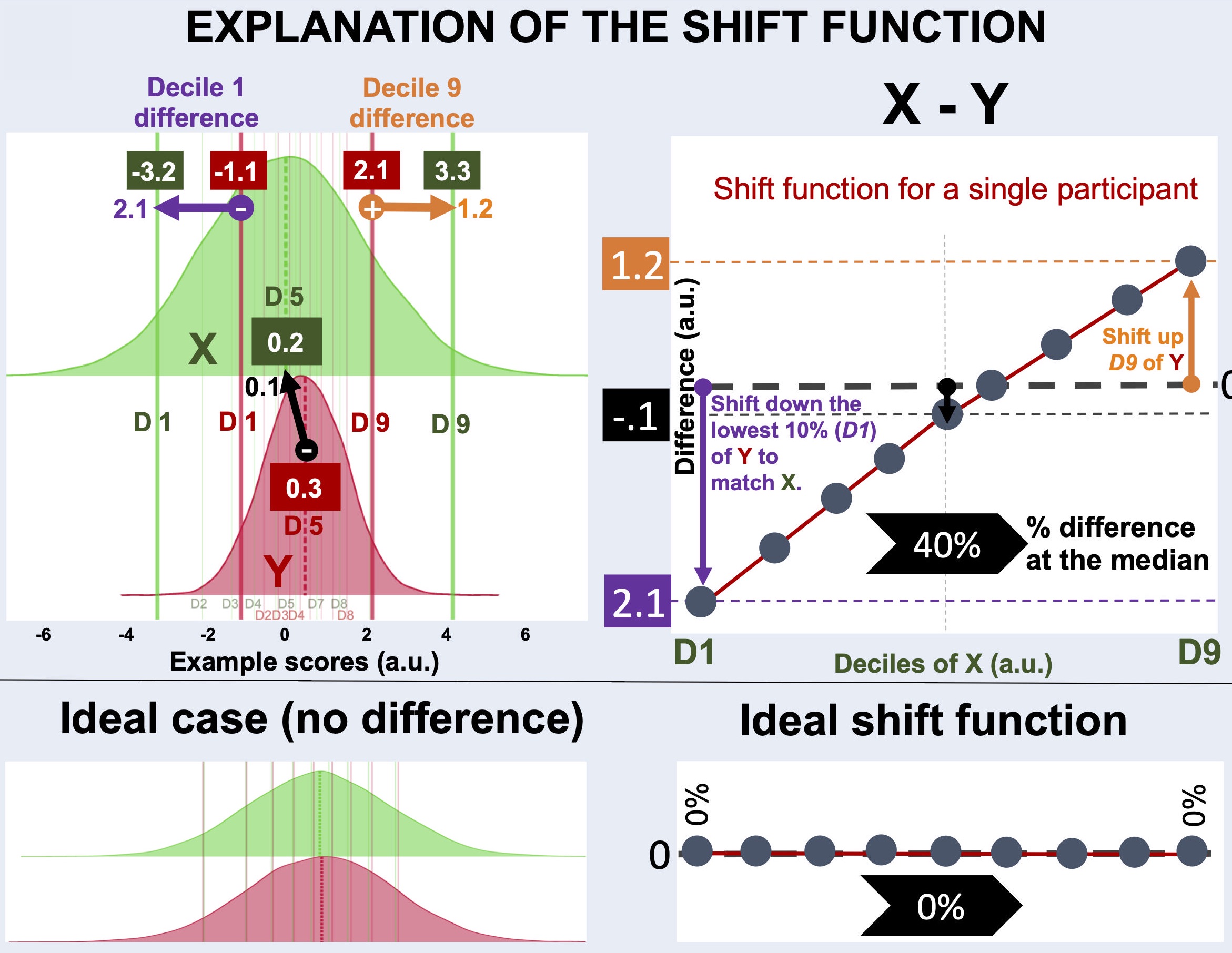
Fig. 4 explanation of the shift function analysis.

What is a decile?

Deciles (a.k.a quantiles) are 1/10th of a distribution, created by splitting the distribution at 9 boundary points (excluding the min and max). For example, median is the 5th decile of a distribution.

How do deciles create a shift function?

To characterize differences between two distributions not only at one decile (e.g., the median), but throughout the whole range of the distributions, shift functions calculate differences at each decile.

For example, distributions X (green) and Y (red) below do not differ much at the central tendency, marked by the dashed lines. The distribution Y is slightly higher than X at the central decile.

On the other hand, distributions X and Y differ in spread. The distribution X is much wider than the distribution Y. As a result:

• The first decile of X (green vertical line on the left) is smaller than that of Y (red vertical line on the left)

• The last decile of X (green vertical line on the right) is greater than that of Y (red vertical line on the right)

The profile of shift function calculated for X - Y explains how the deciles of distribution X should be shifted to match those of the distribution Y:

• The first decile of Y (D1) must be shifted towards left (towards lower values) to match that of X

• The first decile of Y must be shifted towards right (towards higher values) to match that of X

Therefore, the first decile on Fig. 4 is below and the last decile is above the zero-crossing.

See Also

For a more detailed explanation on shift functions, please see this blog post by Guillaume A. Rousselet.

from scipy.stats import norm
# generate random numbers from N(0,1)

fig = go.Figure()


data_normal = norm.rvs(size=10000,loc=0.5,scale=1)
data_normal2 = norm.rvs(size=10000,loc=0,scale=2)

# Figure for ideal case 
#data_normal = norm.rvs(size=10000,loc=0,scale=1)
#data_normal2 = norm.rvs(size=10000,loc=0,scale=1)

fig.add_trace(go.Violin(x=data_normal,
    opacity = 1,    
    line_color= "crimson",
    side="positive",
    name = "Y",
    meanline=dict(visible=True,color="crimson",width=4),
    width=2
))
fig.add_trace(go.Violin(x=data_normal2,
    marker=dict(
    opacity = 0.3,    
    outliercolor='rgba(255, 255, 255, 0.6)',
    line=dict(
        outliercolor='rgba(219, 64, 82, 0.6)',
        outlierwidth=2)),
    line_color= "limegreen",
    side="positive",
    name = "X",
    meanline=dict(visible=True,color="limegreen",width=4),
    width=2                    
))


fig.update_traces(orientation='h')
fig.update_layout(paper_bgcolor = 'white',plot_bgcolor = 'white',height=600, width=800)
fig.update_traces(points=False)
qs = pd.qcut(data_normal2, 10, labels=False)
aa = []
for ii in range(10):
    aa.append(np.median(data_normal2[qs==ii]))
fig.add_vrect(
    x0=aa[9] + 0.8, x1=aa[9]+0.9,
    fillcolor="limegreen", opacity=0.7,
    layer="above", line_width=0,
)

for ii in range(0,9,1):
    fig.add_vrect(
    x0=aa[ii], x1=aa[ii] + 0.02,
    fillcolor="limegreen", opacity=0.3,
    layer="above", line_width=0)
fig.add_vrect(
    x0=aa[0], x1=aa[0] + 0.1,
    fillcolor="limegreen", opacity=0.7,
    layer="above", line_width=0,
)
qs = pd.qcut(data_normal, 10, labels=False)
aa = []
for ii in range(10):
    aa.append(np.median(data_normal[qs==ii]))  
fig.add_vrect(
    x0=aa[9], x1=aa[9]+0.1,
    fillcolor="crimson", opacity=0.7,
    layer="above", line_width=0,
)
fig.add_vrect(
    x0=aa[0], x1=aa[0]+0.1,
    fillcolor="crimson", opacity=0.7,
    layer="above", line_width=0,
)
for ii in range(0,9,1):
    fig.add_vrect(
    x0=aa[ii], x1=aa[ii] + 0.02,
    fillcolor="crimson", opacity=0.3,
    layer="above", line_width=0)
    
fig.add_annotation(x=aa[0], y=0.8,
            text="<b><-- D1</b>",
            showarrow=False,
            yshift=10)
fig.add_annotation(x=aa[-1], y=0.8,
            text="<b>D9--></b>",
            showarrow=False,
            yshift=10)



fig.show()

What about hierarchical shift functions?

Hierarchical shift function (HSF) is an extension of the shift function analysis for the comparison of dependent distributions across multiple participants.

In our case, each between-scanner comparison comes from a repeated measurement, given that the same participants were scanned using different scanners and pulse sequence implementations.

See Also

For a more detailed explanation on shift functions, please see this blog post by Guillaume A. Rousselet.

previous

T1 accuracy & inter-vendor agreement

next

Shift function analysis